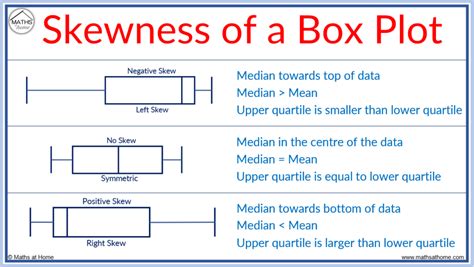
can you use a box plot for non normal distribution We know our data should fit a non-normal (positively skewed) distribution. It should resemble a ski-slope like the picture below: In this post, I will cover five simple steps to understand the capability of a non-normal process to meet .
Metal boxes must be used with metallic cables or conduit. Answers based on the National Electrical Code. Local amendments may apply. Check with your local building officials. Remember Junction boxes have to be accessible. .
0 · skewed to the right boxplot
1 · positively skewed distribution box plot
2 · positively skewed box plots
3 · positive skew vs negative boxplot
4 · how to interpret boxplot results
5 · boxplot skewed to the left
6 · box and whiskers chart explained
7 · 25th percentile on a boxplot
The only time you’re allowed to stop in a yellow box is when you are turning right. You must still make sure your exit road is clear, but you may have to wait for a gap in oncoming traffic before actually turning. If that’s the case, .
skewed to the right boxplot
If you'd like to use a boxplot for other reasons, note that you could compute the expected value from the distribution (ie, fitting, like you mentioned) and then add a marker to the boxplot where peak of the distribution is.Using violin plots, for instance, give you a detailed view of the kernel density of your distribution, and thus highlight "better" the underlying distributions compared to boxplots. In R, you can use .
positively skewed distribution box plot
Data do not have to be normally distributed before a control chart can be used – including the individuals control chart. But, you better not ignore the distribution in deciding how to interpret .
In the last section, we went over a boxplot on a normal distribution, but as you obviously won’t always have an underlying normal distribution, let’s go over how to utilize a .
Testing if a data sample is normally distribution can be done in a lot of ways. One simple method is with a QQ plot. To do this, use 'qqplot(X)' where X is your data sample. If the result is approximately a straight line, the sample is normal. If .
We know our data should fit a non-normal (positively skewed) distribution. It should resemble a ski-slope like the picture below: In this post, I will cover five simple steps to understand the capability of a non-normal process to meet .
A box plot (aka box and whisker plot) uses boxes and lines to depict the distributions of one or more groups of numeric data. Box limits indicate the range of the central 50% of the data, with .Create a box plot for the data from each variable and decide, based on that box plot, whether the distribution of values is normal, skewed to the left, or skewed to the right, and estimate the .
In a boxplot, outliers are plotted individually as dots. A uniform distribution has no 'tails', and outliers are rare. A normal distribution has long thin tails, and and a boxplot of a .
positively skewed box plots
If you'd like to use a boxplot for other reasons, note that you could compute the expected value from the distribution (ie, fitting, like you mentioned) and then add a marker to the boxplot where peak of the distribution is.Using violin plots, for instance, give you a detailed view of the kernel density of your distribution, and thus highlight "better" the underlying distributions compared to boxplots. In R, you can use the ggplot2 library, and use a geom_violin() layer.A normal probability plot is an excellent way to compare an empirical distribution to a normal distribution. Its merits are that it clearly displays the nature of any deviations from normality: ideally, the points lie along the diagonal; vertical deviations .Use a box plot to compare distributions when you have a categorical grouping variable and a continuous outcome variable. The levels of the categorical variables form the groups in your data, and the researchers measure the continuous variable.

The raw data can be shown using q-q-plots, as you do, or using the ECDF, as Frank Harrell suggests. However, I don't think a rug plot will be very enlightening, because of the sheer concentration of 83% of your data points in the interval $[101,428; 101,436]$.Data do not have to be normally distributed before a control chart can be used – including the individuals control chart. But, you better not ignore the distribution in deciding how to interpret the control chart. In the last section, we went over a boxplot on a normal distribution, but as you obviously won’t always have an underlying normal distribution, let’s go over how to utilize a boxplot on a real dataset.
Testing if a data sample is normally distribution can be done in a lot of ways. One simple method is with a QQ plot. To do this, use 'qqplot(X)' where X is your data sample. If the result is approximately a straight line, the sample is normal. If the result is not a .
We know our data should fit a non-normal (positively skewed) distribution. It should resemble a ski-slope like the picture below: In this post, I will cover five simple steps to understand the capability of a non-normal process to meet customer demands.
A box plot (aka box and whisker plot) uses boxes and lines to depict the distributions of one or more groups of numeric data. Box limits indicate the range of the central 50% of the data, with a central line marking the median value. If you'd like to use a boxplot for other reasons, note that you could compute the expected value from the distribution (ie, fitting, like you mentioned) and then add a marker to the boxplot where peak of the distribution is.Using violin plots, for instance, give you a detailed view of the kernel density of your distribution, and thus highlight "better" the underlying distributions compared to boxplots. In R, you can use the ggplot2 library, and use a geom_violin() layer.A normal probability plot is an excellent way to compare an empirical distribution to a normal distribution. Its merits are that it clearly displays the nature of any deviations from normality: ideally, the points lie along the diagonal; vertical deviations .
Use a box plot to compare distributions when you have a categorical grouping variable and a continuous outcome variable. The levels of the categorical variables form the groups in your data, and the researchers measure the continuous variable. The raw data can be shown using q-q-plots, as you do, or using the ECDF, as Frank Harrell suggests. However, I don't think a rug plot will be very enlightening, because of the sheer concentration of 83% of your data points in the interval $[101,428; 101,436]$.
Data do not have to be normally distributed before a control chart can be used – including the individuals control chart. But, you better not ignore the distribution in deciding how to interpret the control chart. In the last section, we went over a boxplot on a normal distribution, but as you obviously won’t always have an underlying normal distribution, let’s go over how to utilize a boxplot on a real dataset.Testing if a data sample is normally distribution can be done in a lot of ways. One simple method is with a QQ plot. To do this, use 'qqplot(X)' where X is your data sample. If the result is approximately a straight line, the sample is normal. If the result is not a .We know our data should fit a non-normal (positively skewed) distribution. It should resemble a ski-slope like the picture below: In this post, I will cover five simple steps to understand the capability of a non-normal process to meet customer demands.
metal fabrication gloves
positive skew vs negative boxplot
how to interpret boxplot results
boxplot skewed to the left
$32.99
can you use a box plot for non normal distribution|25th percentile on a boxplot